MUSA 硬件架构与 GPU 并行程序基础
2024-05-11
1. 引言
近几年来,AI 技术和 GPU 等算力硬件相辅相成相互促进地迅猛发展。如今 AI 技术的应用已经在生活中随处可见,让人们开始意识到元宇宙的概念不是遥不可及。元宇宙这个大目标框架下,AI 技术还有非常广阔的发展空间。为了支撑该技术,以 GPU 为首的算力底座硬件也在不断更新。摩尔线程 GPU(Moore Threads GPU, 简称MTGPU)作为全功能 GPU,拥有图形显示和计算这构筑元宇宙的两大功能,为了实现这一点摩尔线程设计出元计算统一系统架构(Meta-computing Unified System Architecture, 简称 MUSA),其底层框架提供对当今主流显示,高性能计算及 AI 应用库的兼容支持,让开发者能十分方便的在 MTGPU 算力底座上搭建元宇宙应用。
本文着重讨论 GPU 的计算部分。向初学者介绍,计算任务使用 GPU 和 CPU 的区别,什么样的计算任务适合在 GPU 中计算,怎样才能充分发挥 GPU 的性能。
2. MTGPU 硬件架构
2.1. CPU 和 GPU 芯片的简单对比
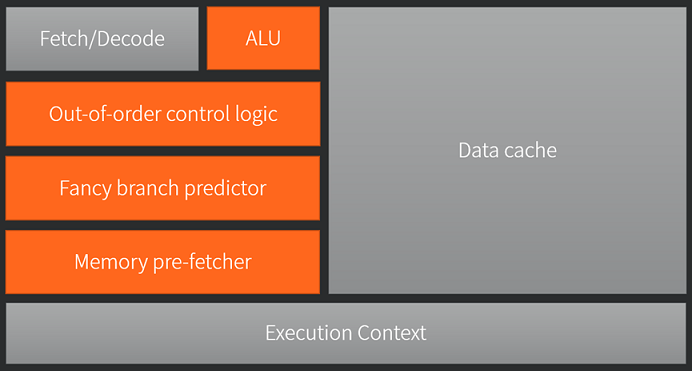
图为 CPU 的典型架构。CPU 是计算机的运算核心和控制核心。它最主要的工作是对输入的数据,进行人们想做的任何运算,再将加工后的数据输出。一个现代通用计算机,通用的意思是能以可编程的方式完成任何任务。具体实现就是运算单元会根据指令完成不同的基本运算,通过指令的组合来完成更加高级的任务。因此 CPU 中,有基本的运算单元,还有传达指令的译码器。现代系统需要 CPU 能并发处理多任务,那么就要由一个管理者,他能这能有条不紊地分批任务,这是一个任务调度器。图中可以看到有很大的面积用于缓存,对于经常重复使用的数据,会从内存读取并暂存在缓存区域中,避免了后续每次使用都要从内存中读取,极大的提升了效率,毕竟从内存读取数据消耗的时间是远远大于计算使用的时间的。最后现代 CPU 还有乱序执行,分支预测,数据预取等高级模块。

上图为 GPU 芯片的典型架构,基本上就只保留了必要的译码单元,缓存,运算单元和任务调度,当然实际的芯片还有其他功能模块,但是他们都没有 CPU 的模块功能复杂。两个简图可以看到 GPU 芯片和 CPU 芯片的主要差别在于 GPU 的运算单元数目远多�于 CPU 运算单元数目,但CPU拥有其他更复杂的功能模块以及 CPU 的单个运算单元的计算能力更强大
2.2. MTGPU 春晓架构介绍
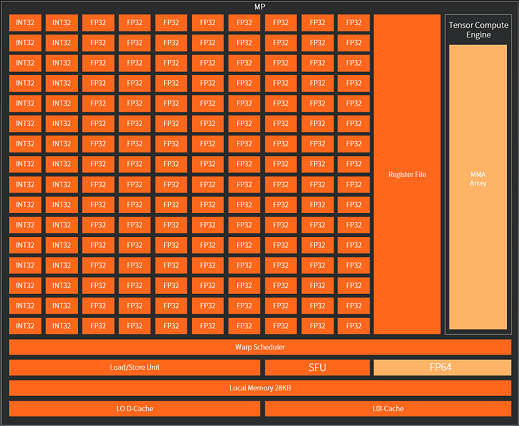
真实的 GPU 架构稍微复杂,一般具有更丰富的层级结构。以春晓架构为例,该架构是产品 MTT S80 的架构。如上图所示,MP(MUSA Processor)是最小的一个整体结构,它含有128个单精度浮点运算单元 FP32,32个整型/位运算单元 INT8,寄存器区域及任务调度区域。除此之外还有32个单精度浮点特殊函数计算单元 SFU,2个双精度浮点运算单元 FP64,张量积算引擎部分 TCE(Tensor Compute Engine)。另外还有28 KB大小的局部储存器 Local Memory。

2个 MP 组成一个 MPX(MUSA Processor eXecution engine),每个 MPX 中的所有 MP 共享24KB的 L1 缓存。2个 MPX 组成一个 MPC(MUSA Processor Cluster),每个 MPC 中所有 MPX 共享512 KB的L2缓存。整个 GP U封装了8个 MPC,通过大小为 16384 KB 的 L3 缓存(也叫Last Level Cache,简称LLC)连接至显存。可以计算得到春晓GPU总共拥有单精度计算核心数目为 4096=8×2×2×128。
2.3. CPU 和 GPU 的典型参数
| Intel Xeon 8280 CPU | MTT S80 GPU | |
|---|---|---|
| 主频 | 2.7 GHz | 1.8 GHz |
| 核心数目 | 28 | 4096 |
| 访存带宽 | 140 GB/s | 448 GB/s |
| 访存延迟 | 89 ns | 400 ns |
| 单精度浮点算力 | 4.8 TFlops | 14.7 TFlops |
| 等效并发线程数 | 1792 | 196608 |
上面表格中给出了计算任务所关心的硬件参数,其中前四个是直接查阅获取的。现在对后面的两个参数做详细说明,他们在 CPU 和 GPU 的计算方法均有所不同。
CPU 的单精度浮点算力。该 CPU 支持 AVX-512指令集,并且有2个 AVX-512 FMA 单元。FMA 乘加运算算作2次浮点运算。AVX-512 指令等价 512 位,即512/32=16个单精度浮点向量。于是单核单时钟周期执行的等效浮点运算数为2×2×16=64 。考虑到主频及核心数目,可以得到总算力为 2.7 GHz×28×64≈4.8 TFlops。
GPU 的单精度浮点算力。只需简单考虑单核单时钟周期浮点运算次数是 FMA 的2次。算入主频及核心数目,总算力为 1.8 GHz×4096×2≈14.7 TFlops 。
CPU 的等效并发线程数,28个核每个核超线程处理2个线程共等效56线程。2个AVX-512 FMA 单元的16个单精度浮点向量计算,等效总线程为 56×2×16=1792。
GPU 的等效并发线程数,MTT S80 允许任务队列最多安排48个 warp,也就是每个核可以并发处理48个任务,则等效并发线程数目为 48×4096=196608。
3. 什么任务适合 GPU 计算
在上一章最后我们给出了 CPU 和 GPU 硬件重要参数的对比,可以看到 CPU 单核的主频是高于 GPU 的,也就是说 CPU 的单核性能毫无疑问比 GPU 的高,但是 GPU 的核心数目远远多于 CPU 的核心数目,在前面的算力计算过程也能看到,正是这个核心数量的差距,使得 GPU 的总算力要远超过 CPU。另外我们可以看到 GPU 的显存访存带宽是要大于 CPU 的内存访存带宽的,这点 GPU 占优。而访存的延时则是 GPU 大 CPU,这点 GPU 不及 CPU。然而访存延迟有什么影响呢?GPU 的访存带宽和算力都大于 CPU,但是实际上真的都使用满了么?从参数看倘若使用率不足三分之一的话,GPU 的性能还不及 CPU 呢。带着这些问题我们进入后面的章节。
3.1. 延时和吞吐
| Intel Xeon 8280 CPU | MTT S80 GPU | |
|---|---|---|
| 核心数目 | 28 | 4096 |
| 访存带宽 | 140 GB/s | 448 GB/s |
| 访存延迟 | 89 ns | 400 ns |
| 延迟内最大传输量 | 12460 bytes | 179200 bytes |
| axpy 串行带宽使用率 | 0.064% | 0.0045% |
| axpy 跑满带宽线程数 | 1558 | 22400 |
| 等效并发线程数 | 1792 | 196608 |
| 线程冗余比例 | 1.2x | 8.8x |
我们将参数表添加几行。其中延迟内最大传输量,表示在访存延迟时间内最大能传输的数据量,等于访存带宽和访存延迟的乘积。我们知道当传输数据量足够大的时候,数据传输时间可以认为是传输数据量除以访存带宽,然而当数据量小到一定程度,访存延迟的负面效应凸显出来。那表中 CPU 的数据看,从内存传数12460 bytes的数据到 CPU 上需要89 ns 的时间,而传输8 bytes 的小数据,也要89 n s时间,这样等效带宽才 8 bytes / 89 ns = 0.09 GB/s。带宽使用率仅 0.064%。
我们来看 axpy 任务,这是最简单的向量乘加任务,也是一个很好展现延迟问题的任务。伪代码如下:
void axpy(float a, float* x, float* y, int n)
{
for(i = 0; i < n; i++)
{
y[i] = a * x[i] + y[i];
}
}
这个例子中,倘若没有任何优化,循环是串行一步步执行的,那么每次执行乘加之前要做的就是从内存获取 x[i] 和 y[i] 两个单精度浮点数,一共8 bytes 的数据。这时就会发生上面所说的问题,对于 CPU 而言访存带宽的使用率才 0.064%,这个问题在 GPU 上会更加严重,由于 GPU 有更高的访存带宽和更高的访存延迟,倘若仅仅单线程执行 axpy 任务,其带宽使用率低至 0.0045%。
为了让显存带宽得到很好的利用,主要的方法就是将程序改成并行程序。简单的说,就是让一个线程执行向量一个元素的乘加,那么对于 CPU 而言跑满带宽需要 12460 bytes / 8 bytes = 1558个线程。而对于 GPU,需要 22400 个线程同时执行才能利用满带宽。就计算规模而言,向量长度大于 1.5K 的 axpy 任务才可能跑满 CPU 带宽,而向量长度大于 22K 的任务才能用满 GPU 带宽,也就是说 GPU 更难将带宽使用满,一般而言需要尺寸规模较大的任务才可能跑满。
我们再看等效并发线程数和 axpy 跑满带宽线程数的对比,不论是 CPU 还是 GPU,可以提供的并发线程数都是大于满带宽所需线程数的,用可用并发线程数和满带宽线程数的比值体现线程冗余比例,可以看到 CP U的设计中,这个冗余比例为1.2倍,是刚好够用的冗余,没有丝毫浪费。但是 GPU 的这个冗余比例确高达8倍。这也是 CPU 和 GPU 架构的区别之一。我们记得前面计算等效并发线程数的方法 CPU 和 GPU 是不同的,CPU 是在核数目的基础上乘了 AVX-512 向量指令的等效处理数目得到的,而 GPU 则是核数的基础上乘上队列最大可使用的 warp 数目。CPU 是靠强大的指令处理更多的事情,而 GPU 仅仅是提供更多的可切换线程,让一个核能在多个线程切换执行达到隐藏访存延迟的效果。
最后我们看在 GPU 上处理延迟问题的另一个思路,除了刚才所说的增加并发线程数目,还可以增加单线程的访存数目,例如将 axpy 写成:
void axpy(float a, float* x, float* y, int n)
{
for(i = 0; i < n; i += 8)
{
y[i] = a * x[i] + y[i];
y[i+1] = a * x[i+1] + y[i+1];
y[i+2] = a * x[i+2] + y[i+2];
y[i+3] = a * x[i+3] + y[i+3];
y[i+4] = a * x[i+4] + y[i+4];
y[i+5] = a * x[i+5] + y[i+5];
y[i+6] = a * x[i+6] + y[i+6];
y[i+7] = a * x[i+7] + y[i+7];
}
}
这个其实就是 CPU 向量指令的思路,在 GPU 上可以用上面手段实现向量化的目的,让 GPU 线程也能在一个访存指令中访问更大的数据,上面的例子中每个线程获取 8×8 bytes=64 bytes 的数据,那么为了跑满带宽,所需的线程数将减少到八分之一。
小结一下,GPU 的架构是一个高吞吐高延迟的,在任务的数据规模较大的情况下才能发挥出其性能,一般任务想要用满 GPU 的访存带宽还是困难的,需要精心设计。
3.2. 任务数据依赖
前面小节可以看出 GPU 是适合并行程序的。为了发挥出 GPU 的性能,就是要让 GPU 尽可能多的核参与到任务当中,足够多的并发线程才能用满显存带宽,发挥 GPU 的优势。这里就引出了一个问题,什么样的任务能很好的并行呢?前面给出的 axpy 的例子就是一个典型的适合并行的程序,我们很容易地安排每个线程处理向量当中的一个元素或多个元素。其中的关键就是,向量乘加计算,向量的每个元素执行是相互独立的,对其他位置的执行没有任何依赖,这样就可以安排所有元素同时执行操作了。这里举个极端的有数据依赖的例子:
void conditionAdd(float* x, float* y, int n)
{
for(i = 0; i < n-1; i++)
{
if (y[i] > 0)
{
y[i+1] = y[i] + x[i];
}
else
{
y[i+1] = y[i] - x[i];
}
}
}
这个例子中,下一步的计算必须等到上一步的计算结果出来才能知道怎么执行,这种有强依赖的计算过程是无法并行的。
一般情况不会那么极端,我们是可以设计出并行计算任务的。我们来看经典的 scan 任务,即求向量的前缀和,输出向量每个元素等于输入向量对应位置前面所有元素之和。
void scan(float* x, float* y, int n)
{
for(i = 1; i < n; i++)
{
y[i] = y[i-1] + x[i];
}
}
初看这个任务和上面提到的极端依赖任务很像,貌似都需要先得到上一个步骤的计算结果才能开始下一个步骤的计算。但是我们可以使用如下图算法:

以八个元素的scan操作为例,使用八个线程进行并行计算,第一步每个线程执行当前位置和前一个位置元素的相加,第二步执行当前位置和前两个位置的元素相加,第三步执行当前位置和前四个位置元素相加。
对于一般性的,共2^N个元素的 scan 操作,需要 N 个步骤,第i步骤执行当前位置元素和前 2^(i-1) 个元素的相加。可以看到如果使用串行依次处理,一共需要进行约2^N个相邻元素加法步骤。倘若用上面的算法,一共要进行N个步骤,步骤数量远小于串行方法。然而这个并行算法总的加法次数却是 N × 2^N。这些加法可以由2^N个线程分担并行执行。这里多出来的加法次数,就是为了并行而��引入的计算冗余。是的,计算冗余是为了在有数据依赖的情况下能并行而产生的必要牺牲。从本质上来说,是为了让线程任务更独立不依赖其他线程的数据,进行了与其等待其他线程任务的数据倒不如自己再算一遍的取舍。计算冗余的思想在 GPU 架构下尤其重要,前面我们看到 GPU 架构中线程数目是大量冗余的,而为了跑满带宽我们需要让尽可能多的核都忙起来,这样计算冗余的牺牲反而是一举两得的。
3.3. 计算强度
前面我们讨论发挥GPU性能,先从访存带宽讲起。有人可能会有疑问,为啥关注带宽呢,一般芯片大力宣传的不是浮点运算算力么,都是听说算力在飞速增长,听说AI需要大量的算力,而带宽却少有人关注。事实却有点违背直觉,单芯片算力增长反而不需要太过关注,因为现在GPU算力已经足够甚至过剩,大多数任务想用满算力比用满带宽要困难的多。
我们来这样考虑,还是以axpy任务为例,一次乘加运算需要读取 8 bytes 的数据。那么在跑满带宽的情况下能做多少次乘加运算呢?容易得出结论,对于 CPU 而言是140GB/s / 8bytes = 17.5 G/s,乘加认为是2次操作,则满带宽算力为 35 GFlops。 同理GPU的满带宽算力仅 112 GFlops。
| Intel Xeon 8280 CPU | MTT S80 GPU | |
|---|---|---|
| 访存带宽 | 140 GB/s | 448 GB/s |
| 单精度浮点算力 | 4.8 TFlops | 14.7 TFlops |
| 满带宽乘加算力 | 35 GFlops | 112 GFlops |
| 计算强度 | 137 | 131 |
�很清楚的看到,不论是 CPU 还是 GPU ,执行向量乘加任务,在带宽打满的情况下,算力的使用率还不到百分之一。我们这里定义计算强度是单精度浮点算力与满带宽单精度乘加算力的比值,他亦表示为了要充分用满算力,我访存获取的每个4 byte单精度浮点数要拿来做几次浮点运算。什么样的任务,读取的数据能反复使用一百多次?
我们先来看一个简单的数据会被多次利用的任务,均值滤波任务,这个任务就是将一个二维的图像,每个像素点的值用它周围像素点的平均值替代,从而达到对图像平滑模糊的效果。
上图是用周围3×3区域9个像素点做平均的例子,根据平滑程度的需要有时也会用周围5×5, 7×7等像素去平均。在这样的任务下,每个像素点的值从内存读取之后,会被周围几个像素点的计算使用到。如5×5的均值滤波任务中,读取一个像素的浮点数,会用以25次加法运算,可以认为计算强度能达到25。
我们可以很容易的估算一个任务的计算强度,直接用完成该任务总共需要的浮点运算次数除以总需要的数据量即可。如 axpy 任务,需要读取x,y向量一共2N个浮点数,每个元素做一次乘加即2次浮点操作,总用做2N次浮点操作,于是 axpy 任务的计算强度就是2N / 2N = 1。对于均值滤波任务,总像素点数量N,需要读取N个浮点数,每个像素点要做k × k次加法和1次乘法,那么计算强度就是N × (k × k + 1) / N = k × k + 1,其中k是周围像素区域的尺寸。
以上两个例子,计算强度都不会随任务数据的规模变化,即使是均值滤波任务,计算强度k × k + 1,在任务参数k确定的情况下也是一个常数,计算强度与N的大小无关。那么在均值滤波任务中,即使取k = 7,计算强度为50,该任务最理想满带宽情况下的算力预计也达不到芯片算力的一半,依然无法充分使用硬件算力。
在计算领域,少有实际任务能够用满芯片的算力的。在能用满算力的任务中,最经典最常用的就是矩阵乘法任务。我们用上面的方法估算一个矩阵乘法任务的计算强度,考虑尺寸是n×k的A矩阵和k×m的B矩阵相乘得到 n×m 的 C 矩阵。需要读取的数据就是两个矩阵所有元素,n×k+k×m=k×(n+m)。结果C矩阵的每个元素是A矩阵行向量和B矩阵列向量的向量内积,即每个元素要执行约k次乘加即2k次浮点运算,总共的浮点运算次数约2k×n×m。所以计算强度为2k×n×m / [k×(n+m)] = 2nm/(n+m)。我们考虑常用的方阵乘积,即 n=m=N, 容易得到计算强度为N。可以看到矩阵乘任务的计算强度不再是常数了,而是随任务规模线性增长。普遍的矩阵乘法矩阵的规模只要上百上千,这个理论的计算强度很容易能达到用满算力的计算强度,这也说明矩阵乘的确理论上能用满芯片算力。
矩阵乘法任务理论计算强度能随计算的数据规模达到非常大,但是不意味着实际能轻易达到。上面的估算方法有一个很强的假设,就是认为从内存一次读取到的所有矩阵数据,能被所有线程在后续计算中都直接使用到。这个假设相当于认为芯片的寄存器有无穷大,从内存搬运来的数据能直接放在寄存器里,提供后续计算一直反复使用。然而寄存器资源是很有限的,不可能做到。退而求其次的就是使用局部储存器 local memory 以及利用好L1缓存,同样这些资源的大小都有限。因此大的矩阵乘法需要拆分成小的矩阵乘法进行计算,通过精心的算法设计,做到每个小的任务能够充分用满浮点运算算力。关于矩阵乘法任务的极致优化,是一个内容很丰富的话题,后续将单独讨论。本文仅从大的角度出发讨论怎样的任务能发挥出 GPU 的性能。
4. 总结
由上面讨论可以看到,矩阵乘任务是适合用GPU进行加速计算的,并且矩阵乘是 AI 技术深度学习中训练及推理的的核心计算。因此 GPU 在 AI 技术的发展中起到了至关重要的作用。事实上,为了专门对AI的任务有更进一步的加速作用,较新的 GPU 还专门开辟了 Tensor core(MTGPU 也叫Tensor Compute Engine)张量计算单元,这些张量计算单元进行矩阵乘运算算力相较于普通运算单元有大幅度提升。关于 Tensor Compute Engine 的细节本文不做深入介绍。

